背包问题笔记

发表于

01背包

问题描述

给定一组物品，每种物品都有自己的重量和价值，现有一个背包，能承受的重量有限，在受限制的重量下，取若干物品，使得总价值最大。这一类问题，被称为背包问题。

当前有 \(N\) 件物品和一个容积为 \(V\) 的背包。已知第 \(i\) 件物品的体积是 \(c_i\)，价值是 \(w_i\) 。 由于每种物品有且仅有一件，因此只能选择放或不放，我们称之为 01 背包问题。 现在你需要选出若干件物品，在它们的重量之和不超过 \(V\) 的条件下，使得价值总和尽可能大。

思路解析

最初级/暴力的算法

给物品随机标上编号，对每个物品，都枚举选/不选两种结果，用搜索遍历所有可能的情况。结果写入一张表中：一列为体积，一列为最大价值。每次枚举都检测当前背包内物体体积和价值，并与表中大于等于该体积对应的价值数据比对，如当前结果更优则更新表中价值。

优化思路

上面写的初级算法运行下来，实际上就形成了搜索树。搜索树的第几行代表着有几个物品可供选择，一行中就包含了所有可能出现的情况。我们现在想要做的，无非就是尝试减少不必要的结果的出现。

为了方便我们找到「不必要的结果」，我们需要把被舍弃的（也就是被更新掉的）情况与被保留的进行比较。并且显然要简化掉搜索树的整一行是几乎不可能的，所以我们要选择BFS搜索而不是DFS搜索。

很自然地，我们会发现，在同一行中会出现两个总体积相同而总价值不同的情况。又因为对这样的两个节点生成子节点的方式是相同的，自然应该舍弃价值较小的那一个节点了。但是这还不够，我们又发现甚至还有些节点的总体积比另一些要小，总价值反而还更大了，这怎么办呢？如果把节点都拿出来再这样一点一点比对、舍弃，还是太麻烦了。有没有什么办法能够在写下节点时，就看出这个节点够不够好呢？

为了解决这个问题，我们可以尝试把体积变得更加「连续」。也就是我们把不在节点中出现的背包容量也写下来，从0, 1, 2, 3, ..., \(V\)列成一个表格。那么在每写一个节点时，我们就把表格中大于等于节点体积的格子都遍历一遍，如果这个节点的价值比格子中的价值大，那么就把它替换掉。如果不是，那么就忽略。

鉴于题目本身就对背包容量\(V\)有要求，这个\(V\)本身也是很可能不正好等于要找的最优节点的总体积，我们就完全抛弃BFS搜索，只用表格。具体的解决办法如下：

1.体积和价值是绑定在一起的。题目对总体积有要求，所以求解时限制总体积。

2.在对每一个物品进行遍历时，已知的就是前面已经遍历过的物品在各种体积限制下价值最大化的情况。（最开始是不放任何物品，所以第一行都为零。）我们要做的就是继续列出在各种重量条件下，上面已经遍历过的物品加上这个物品怎样选择能让价值最大。

3.因为体积和价值绑定在一起，价值最大化时总体积越大价值一定越大。填表时只是在决策是否需要放入这个物品。

4.填写每一格时，先看此格对应的总体积是多少，如果总体积还没有决策的物品的体积大，就不可能将这个物品放入，故直接填上一行的情况。当体积足够放入时，比较放或不放的价值哪个更大。假设放入，则价值为「总体积减去物品体积时的最大价值」（直接查上一行的表即可得到）加上这个物品的价值。假设不放，则价值为上一行的价值。

算法展示

动态规划是什么

动态规划（英语：Dynamic programming，简称DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。[1]

如果递归算法反复求解相同的子问题，就称为具有重叠子问题（overlapping subproblems）性质。 在动态规划算法中使用数组来保存子问题的解，这样子问题多次求解的时候可以直接查表不用调用函数递归。[2]

实际上，刚才的思路蕴含的就是动态规划的思想。

图片演示

img1
img1
img2
img2
img3
img3
img4
img4

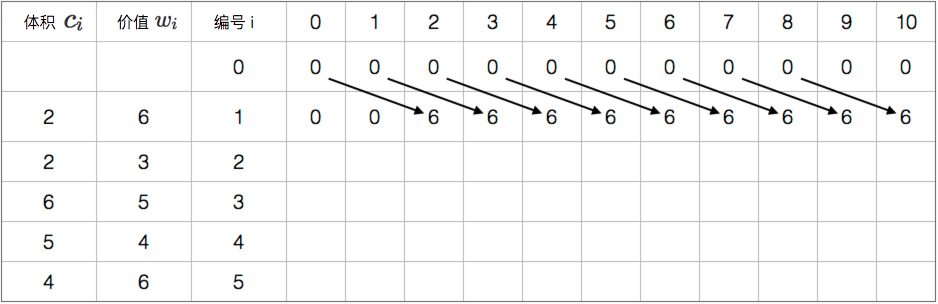
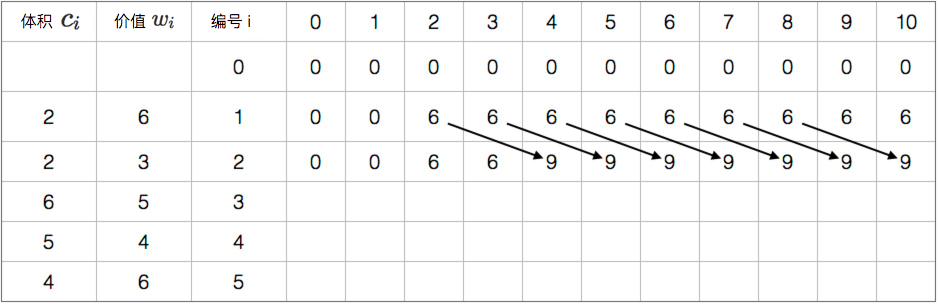
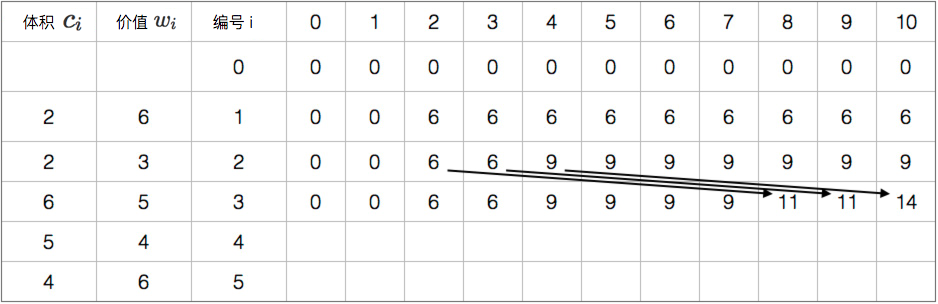
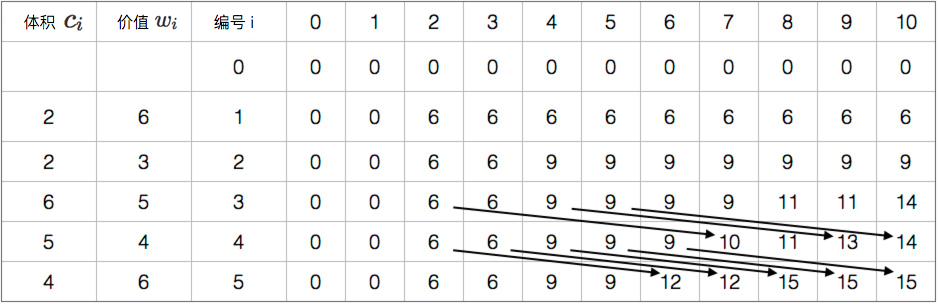
参考代码

来源见[3]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
using namespace std;
int max(int x, int y) {
   return (x > y) ? x : y;
}
int knapSack(int W, int w[], int v[], int n) {
   int i, wt;
   int K[n + 1][W + 1];
   for (i = 0; i <= n; i++) {
      for (wt = 0; wt <= W; wt++) {
         if (i == 0 || wt == 0)
         K[i][wt] = 0;
         else if (w[i - 1] <= wt)
            K[i][wt] = max(v[i - 1] + K[i - 1][wt - w[i - 1]], K[i - 1][wt]);
         else
        K[i][wt] = K[i - 1][wt];
      }
   }
   return K[n][W];
}
int main() {
   cout << "Enter the number of items in a Knapsack:";
   int n, W;
   cin >> n;
   int v[n], w[n];
   for (int i = 0; i < n; i++) {
      cout << "Enter value and weight for item " << i << ":";
      cin >> v[i];
      cin >> w[i];
   }
   cout << "Enter the capacity of knapsack";
   cin >> W;
   cout << knapSack(W, w, v, n);
   return 0;
}

后记

有些朋友看到我这一篇可能会觉得很惊讶，因为这一篇和以前的那些风格和领域都完全不同。我大概是上一年6月放弃了参加信息学竞赛的想法，而这个博客开始于9月。上一年6月到现在这段时间里，我的很多想法都发生了翻天覆地的变化。现在我又开始重拾信息学了。目前我自己也觉得自己很可能拿不到奖，但是这也无所谓了。我以后会专门把这些文章标上「信息学」的标签，当然除此之外我也会继续写随笔。

多重背包

题目描述

有 \(N\) 种物品，第 \(i\) 种物品的体积是 \(c_i\)，价值是 \(w_i\)，每种物品的数量都是有限的，为 \(n_i\)。

现有容量为 \(V\) 的背包，请你放入若干物品，在总体积不超过 \(V\) 的条件下，使总价值尽可能大。

思路解析

Reference

[1] 动态规划, 维基百科，自由的百科全书

[2] 算法-动态规划 Dynamic Programming--从菜鸟到老鸟, CSDN

[3] C++ Program to Solve Knapsack Problem Using Dynamic Programming

问题描述及图片演示来源于计蒜客，在此感谢。