简析动态规划

发表于

动态规划是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

动态规划是一种在 OI 中非常常见的算法。如上所述，动态规划的精髓在于子问题，然而并不是所有和子问题相关的算法都是动态规划。要搞清楚动态规划是什么、为什么、怎么用，我们可以从两种方向来认识。

重叠子问题

例题1：

蒜头君很喜欢爬楼梯，这一次，他获得了一个特异功能，每次可以跳跃任意奇数的阶梯。比如他初始在楼底，跨越一个阶梯到达 11 号阶梯，或者跨越 3 个楼梯到达 3 号阶梯。如下图

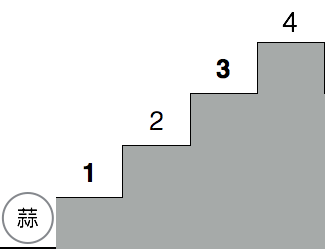
蒜头君爬楼梯
蒜头君爬楼梯

为了选出一种最轻松的爬楼梯的方式，蒜头君想把所有不同的到达楼顶的方式都尝试一遍。对于一共有 \(n\) 个阶梯的楼梯，蒜头君一共有多少种方法从楼底到达楼顶？

最暴力的做法就是递归搜一遍：

1
2
3
4
5
6
7
8
9
10
11
12
typedef long long ll;
ll path(ll n) {
    if (n == 0) {
        return 1;
    } else {
        ll ans = 0;
        for (int i = 1; n - i >= 0; i += 2) {
            ans += path(n - i);
        }
        return ans;
    }
}

时间复杂度 \(O(n!)\)，但其实这离答案就差一点。

Tips: 你要知道第 \(n\) 个阶梯的方案数，你只需要知道到第 \(n-1\), \(n-3\), \(n-5\)…… 个阶梯的方案数。

我怎么知道？存下来就行了呗：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
typedef long long ll;
ll memory[MAXN] = {0};
ll path(ll n) {
    if (memory[n]) {
        return memory[n];
    }
    if (n == 0) {
        return 1;
    } else {
        ll ans = 0;
        for (int i = 1; n - i >= 0; i += 2) {
            ans += path(n - i);
        }
        memory[n] = ans;
        return ans;
    }
}

这么一来，时间复杂度就变成 \(O(n)\) 了。

思路：因为 \[ path_{n} =path_{n-1} +path_{n-3}+...+path_{n-(2k-1)} \] 所以用数组记录每个子问题的解以避免重复计算。

这就是重叠子问题，通过对重叠子问题的记忆，可以极大地优化很暴力的算法。

重叠子问题，在编程层面上常常表现为纯函数。如果你曾经接触过函数式编程（比如使用 React 之类的库或者 Haskell 语言），你可能听说过这个概念。纯函数是一个满足以下条件的函数：

  • 输入参数相同时，输出值相同。
  • 不能有语义上可观察的副作用，比如更改输出值以外变量的内容等。

上文所述 path 函数正好满足这些要求。因此，我们可以放心地根据参数缓存它的返回值。

最优子结构

Leetcode 最小路径和

给定一个包含非负整数的 \(m\times n\) 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

同样先用递归写

1
2
3
4
5
6
7
8
9
10
11
12
typedef long long ll;
int min_path(int x, int y) {
    if (x == 1 && y == 1) {
        return grid[x][y];
    } else if (x == 1) {
        return min_path(x, y - 1) + grid[x][y];
    } else if (y == 1) {
        return min_path(x - 1, y) + grid[x][y];
    } else {
        return min(min_path(x - 1, y), min_path(x, y - 1)) + grid[x][y];
    }
}

你现在肯定在想：记忆化！开个数组 min_path[x][y] 把遍历到的结果全存下来，如果已经算过直接返回不就行了！

先等一下，我们先想想，这个 min_path 函数在语义上是什么用途呢？是从 \((1,1)\) 前往 \((x,y)\) 的最小距离。那你怎么就肯定 \((x,y)\) 变了以后，你存下来的还是对应的最短距离呢？

换句话说，记忆化的前提是：无论终点是哪一个，到达终点的路径上的点之间走的全部都是最短距离，不存在有需要绕路的情况。

这就是最优子结构。一个解是最优的，那么它在子问题中也必定是最优的。

再看一道题：

P1541 [NOIP2010 提高组] 乌龟棋

简单写个暴力递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <cstring>
#include <iostream>
using namespace std;
const int MAXN = 351;
const int MAXM = 121;
int a[MAXN];
int b[MAXM];
bool used[MAXM];
int n, m;
int max_scores(int x) {
    if (x == 1) {
        return a[x];
    } else {
        int ans = 0;
        for (int i = 1; i <= m; i++) {
            if (!used[i]) {
                used[i] = true;
                ans = max(ans, max_scores(x - b[i]) + a[x]);
                used[i] = false;
            }
        }
        return ans;
    }
}
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    for (int i = 1; i <= m; i++) {
        cin >> b[i];
    }
    memset(used, 0, sizeof(used));
    cout << max_scores(n);
}

这时候，还能记忆化吗？

不行了。因为函数返回的值不但跟终点位置 x 有关，还跟使用爬行卡片情况的数组 used 有关。显然，这个函数不满足上面所说纯函数的两个要求。如果你把 used 也当成参数加进来，那么每次 used 的值都会不同，记忆化没有意义。

这是为什么呢？原因就是现在我们的函数 max_scores(int x) 不具有最优子结构了。当前贪心地把前 x 个格子的分数拿到最大用掉了爬行卡片，后面就会受影响得不到最优的结果。正是因为有了最优子结构，子问题才会重叠。最优子结构是因，重叠子问题是果。

那，这题就不能用动态规划做了？

仔细观察题目：

分成4种不同的类型（\(M\) 张卡片中不一定包含所有 4 种类型的卡片，见样例），每种类型的卡片上分别标有 1, 2, 3, 4 四个数字之一。

总共只有四种类型的卡片，而相同数字的卡片没有任何区别。重叠子问题！写一下试试：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <algorithm>
#include <cstring>
#include <iostream>
using namespace std;
const int MAXN = 351;
const int MAXM = 121;
const int MAXB = 41;
int score[MAXN];
int n, m;
int memory[MAXB][MAXB][MAXB][MAXB];
int max_scores(int* use) {
    if (memory[use[0]][use[1]][use[2]][use[3]]) {
        return memory[use[0]][use[1]][use[2]][use[3]];
    }
    if (use[0] == 0 && use[1] == 0 && use[2] == 0 && use[3] == 0) {
        return score[1];
    } else {
        int ans = 0;
        int x = 1;  // start from 1
        for (int i = 0; i < 4; i++) {
            x += use[i] * (i + 1);
        }
        for (int i = 0; i < 4; i++) {
            if (use[i] != 0) {
                use[i]--;
                ans = max(ans, max_scores(use) + score[x]);
                use[i]++;
            }
        }
        memory[use[0]][use[1]][use[2]][use[3]] = ans;
        return ans;
    }
}
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> score[i];
    }
    int b;
    int cnt[4] = {0, 0, 0, 0};
    for (int i = 1; i <= m; i++) {
        cin >> b;
        cnt[--b]++;
    }
    cout << max_scores(cnt);
}

顺利 AC. 我们可以发现，选取递归函数的参数和语义是解决此问题的关键。

虽然这个函数在形式上仍然不满足纯函数的要求，但是这仅仅是为了方便。你完全可以用更加啰嗦的形式，将参数由一个数组指针改成四个整型，把这个函数改造成一个纯函数。

形式不重要

动态规划在狭义上一般都是从最小的子问题开始，一步一步求解更大规模的问题，所以它的实现都是循环，而不是递归。然而，上面讲的全部都是递归，这种方法会被单独称作记忆化搜索。但是我这么做的原因正是想说明一点：形式不重要，重要的是子问题的解之间的依赖关系。

这里引用知乎上的一篇回答：

动态规划的初衷是，

通过找到合适的角度，将所求解的目标值在某（几）个维度上展开，使得最终的目标能变成一个函数在某组自变量下的值：比如在经典题目数字三角形中，将“和”在“横纵坐标”上展开，那么最终的目标就是 \(max\{f(n - 1, i)\}\)，\(i\) 从 \(0\) 到 \(n-1\).

这种展开需要满足的性质是：首先，展开后，函数值是可以由自变量唯一确定的；其次，函数有一种递推表达式；最后，可以通过某种求值顺序（待求的所有函数值的依赖关系形成一个有向无环图），从显然的初值开始依次求，直到目标值。

至于是用循环解，还是记忆化搜索解，还是用 BFS 或者 DFS 解，都不本质。这个依赖于上文所说的有向无环图的结构。

而求解这个问题，正是遍历这张有向无环图上和答案点直接或间接相连的所有点。

我们可以用最暴力的方法去递归，这就对应着在那个有向无环图中从我们要求解的那个点开始，完全按照有向边走。可以想见，这么走必定会大量重复经过点，这就是它低效的原因。

那我们可以怎么优化呢？记忆化搜索给出的答案是把走过的点的结果存起来，下一次就不往下走了，这样就避免了绝大部分重复经过的情况。

而使用循环的动态规划则是从最底部已知的边界点开始，倒着往上遍历。它并不依赖图之间的有向边遍历，而是按照预设好的路线遍历。这就需要保证遍历到的每个点的依赖都已被遍历。

所以说，能用动态规划求解的问题一定能用记忆化搜索求解。

计算机只会穷举。所有算法都是在充分利用给定的条件，让计算机更优雅地穷举。